团队简介:主要从事微分方程表示的孤立子、呼吸子、怪波等非线性方程的相关理论与应用研究,以及分数阶方程的数值计算和应用研究。主持国家自然科学基金项目、江苏省自然科学基金项目、中国博士后基金项目等省部级研究项目14项,在Automatica、Chaos, Solitons & Fractals、Calcolo等期刊上发表高水平论文50余篇,出版专著1部,获教育部高等学校科学研究优秀成果奖自然科学奖二等奖1项,江苏省高等学校科学技术研究成果奖二等奖2项、三等奖2项。
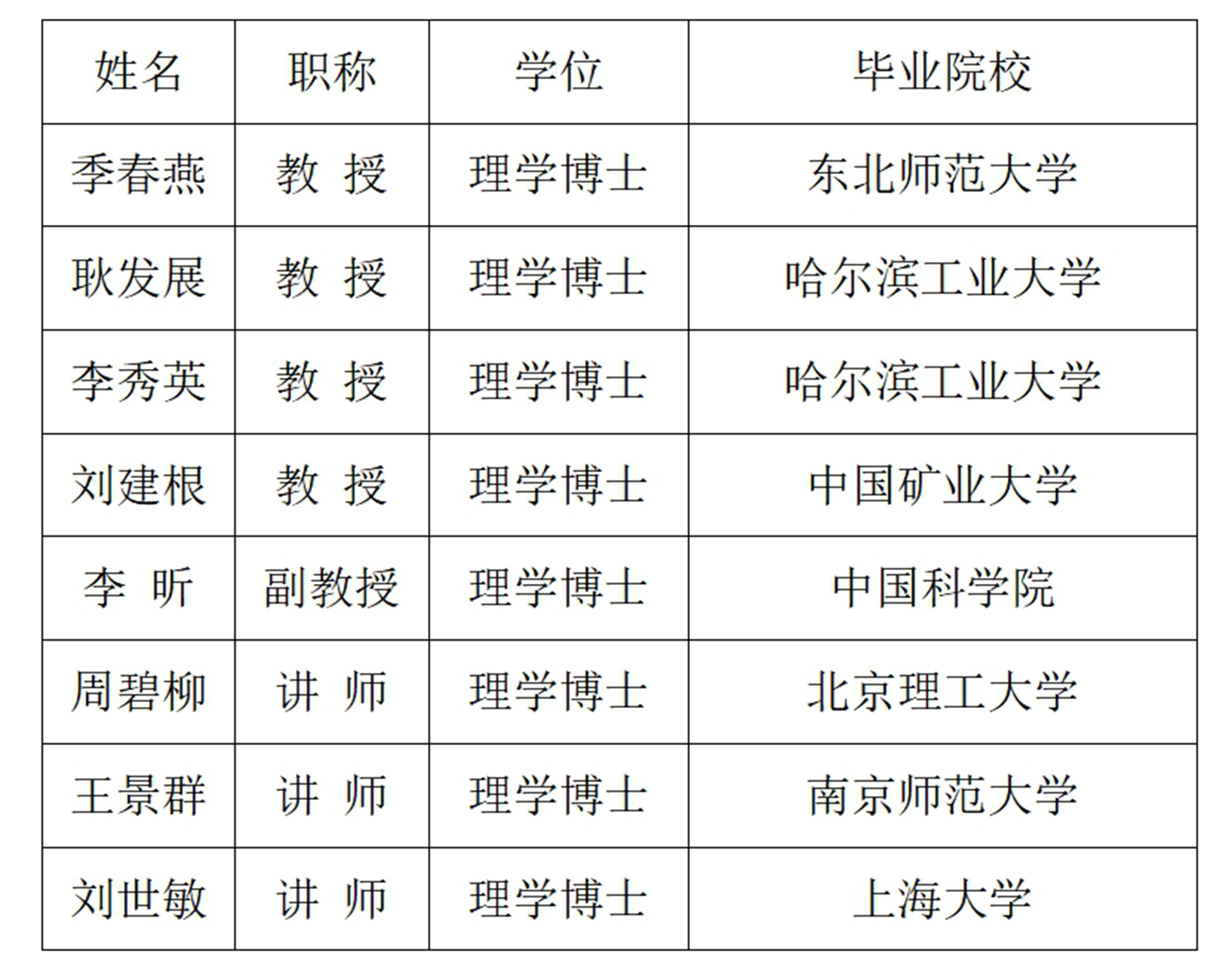
团队骨干:
研究内容:
1.基于再生核希尔伯特空间理论的分数阶奇异摄动问题数值分析:分数阶奇异摄动问题解的边界层、内部层效应,以及分数阶算子的非局部性,决定了分数阶奇异摄动问题数值分析的研究具有很大的挑战性。再生核希尔伯特空间是研究函数逼近、分数阶问题数值分析和系统识别比较理想的空间框架,在此空间理论框架下,研究分数阶奇异摄动问题的有效数值方法和分数阶奇异摄动系统鲁棒的识别方法。
2. 时空分数阶孤子方程的公式化、高阶对称及近似守恒律:一类具有物理背景意义的高维非线性分数阶孤子方程模型在流体力学、计算力学、数学等领域都扮演着重要的角色。通过研究发展分数阶Lie对称群理论等研究高维非线性分数阶孤子方程的对称、相似约化和最优系统等可积性指标和它们的精确解及其动力学行为。
3. 双线性方法在非零背景下的孤子方程中的应用:具有非零背景的可积系统在数学物理模型中自然存在,如非线性薛定谔方程在非零背景下产生怪波。由于非零背景的存在,使得孤子方程的求解变得更加复杂,具有任意非零背景的孤子方程的双线性形式的研究也具有一定的挑战性。致力于研究双线性方法下的具有非零背景的孤子方程及其非局部形式的Wronskian解和解的渐近分析。
4.可积系统呼吸子和怪波的理论分析以及数值计算:基于非线性发展方程自身的复杂性,将利用双线性直接方法、稳定性分析、谱分析和一些数值代数算法等来研究一些可积系统呼吸子解及其相关性质,构造高效、稳定的数值算法和有效的稳定性测试技巧,丰富可积系统的应用。
5.广义PT-对称高次非线性波系统的孤子稳定性及动力学分析:具有高阶、高次项和PT-对称势的非线性波系统具有丰富的性质和理论研究价值,我们主要采用解析方法与数值方法相结合、定性分析和定量计算相结合的方式对具有PT-对称势广义四阶导数非线性Schrödinger方程展开研究,为相应的物理实验提供数据和理论支撑。
6.三维分段非线性系统全局动力学解析方法及其应用:由于分段非线性的存在,研究该类系统的全局动力学非常棘手。目前,采用解析方法研究三维分段非线性系统全局动力学的工作较少,而将解析的非光滑全局分析方法由平面分段线性系统发展到空间分段非线性系统,需要引入李代数方法和不变纤维丛理论来突破空间轨道几何描述上的瓶颈。因此,主要致力于研究三维分段非线性系统全局动力学的解析方法及其应用。
7.随机发展方程的动力学行为研究:发展方程在物理、化学、生物、经济和工程等领域都有很重要的应用,在自然界中,环境噪声也无时无刻存在。随机发展方程的研究引起了极大关注。本项目致力于研究随机发展方程(如随机Navier-Stokes方程、随机Navier-Stokes-Oseen 方程,带有Coriolis力的随机Navier-Stokes方程等)的动力学行为,揭示环境噪声对随机发展方程的内在影响及其本质特征。
8. 函数型数据分析的核方法及其在分数阶系统识别中的应用:函数型数据具有无穷维的特征,传统的多元统计方法不再适用于这类数据的分析。由于分数阶微积分算子的非局部性,分数阶系统识别的研究比整数阶系统识别要复杂得多。首先我们研究高维函数型数据参数回归和函数型数据非参数回归的稳健的核方法,在此基础上,结合分数阶理论,研究分数阶系统识别的鲁棒的核方法。
代表性论文:
1. F.Z. Geng, X.Y. Wu.Reproducing kernel-based piecewise methods for efficiently solving oscillatory systems of second-order initial value problems, Calcolo,2023, 62(2):1-20.
2. F.Z. Geng, X.Y. Wu. Kernel functions-based approach for distributed order diffusion equations, Numerical Methods for Partial Differential Equations,2021, 37(2):1269-1281.
3. X.Y. Li, Joel A. Rosenfeld. Fractional Order System Identification With Occupation Kernel Regression, IEEE Control Systems Letters,2022, 6: 19-24.
4. X.Y. Li, B.Y. Wu. A stable and efficient technique for linear boundary value problems by applying kernel functions, 2022, Applied Numerical Mathematics,172:206-214.
5. C.Y. Ji,X.Yang,Y.Li.Permanence, extinction and periodicity to a stochastic competitive model with Infinite distributed delays, Journal of Dynamics and Differential Equations, 2020, 2021(33): 135-176.
6. C.Y.Ji,X.Yang,Y. Li.Periodic solutions for SDEs through upper and lower solutions, Discrete and Continuous Dynamical Systems-B, 2020, 2 5(12): 4737-4754.
7. C.Y.Ji,D.Q.Jiang,Q.S.Yang,N.Z.Shi.Dynamics of a multigroup SIR epidemic model with stochastic perturbation, Automatica, 2012, 4 8(1): 121-131.
8. J.G.Liu, F.Z,Geng. An explanation on four new definitions of fractional operators, Acta Mathematica Scientia, 2024, 44B(4): 1-9.
9. J.G.Liu, X.J.Yang. Symmetry group analysis of several coupled fractional partial differential equations, Chaos, Solitons & Fractals, 2023, 173: 113603.
10. J.G.Liu, X.J.Yang, Y.Y.Feng, P.Cui. On group analysis of the time fractional extended (2+1)-dimensional Zakharov-Kuznetsov equation in quantum magneto-plasmas, Mathematics and Computers in Simulation, 2020, 178: 407-421.
11.X.Li, L.Wang, Z.J.Zhou, Y.Chen, Z.Y.Yan.Stable dynamics and excitations of single-and double-hump solitons in the Kerr nonlinear media with PT-symmetric HHG potentials, Nonlinear Dynamics, 2022, 108: 4045-4056.
12. X.Li, Z.Y.Yan.Stability, integrability, and nonlinear dynamics of PT-symmetric optical couplers with cubic cross-interactions or cubic-quintic nonlinearities,Chaos, 2017, 27: 013105.
13. B.L.Zhou, Y.F.Jin, et al. Global dynamics for a class of tristable system with negative stiffness, Chaos, Solitons & Fractals, 2022, 162: 112509.
14. B.L.Zhou, Y.F.Jin, et al. Subharmonic resonance and chaos for a class of vibration isolation system with two pairs of oblique springs, Applied Mathematical Modelling, 2022, 108: 427-444.
15. B.L.Zhou, H.B.Chen, et al. Harmonic solutions for a class of non-autonomous piecewise linear oscillators, Communications in Nonlinear Science and NumericalSimulation, 2021, 102: 105912.
16. J.Q. Wang, L. Tian,B.Guo, Y. Zhang. Nonlinear stability of breather solutions to the coupled modified Korteweg-de Vries equations, Communications in Nonlinear Science and Numerical Simulation,2020,90: 105367.
17. J.Q. Wang, L.Tian, W.Guo. Global exact controllability and asympotic stabilization of the periodic two-component µρ-Hunter-Saxton system, Discrete and Continuous Dynamical Systems Series S, 2016, 9 (6): 2129-2149.
18. S.M. Liu, J. Wang, D.J. Zhang. Solutions to Integrable Space-Time Shifted Nonlocal Equations, Reports on Mathematical Physics, 2022, 89(2): 199-220.
19. S.M. Liu, W. Hua, D.J. Zhang. New Dynamics of the Classical and Nonlocal Gross-Pitaevskii Equation with a Parabolic Potential, Reports on Mathematical Physics, 2020, 86(3): 271-292.

