研究领域：致力于声学功能材料的设计理论与优化方法、声子晶体中声光调控与耦合作用、非线性声学与空泡动力学理论、无损检测理论及其关键技术等方面的研究工作。近年来，承担国家自然科学基金重大研究计划子课题、江苏省自然科学基金省市联合资助项目子课题、企业委托攻关项目等各类项目10余项，在NDT and E International、Applied Physics Letters、Journal of The Acoustical Society of America等期刊发表高水平论文30余篇。

团队成员：

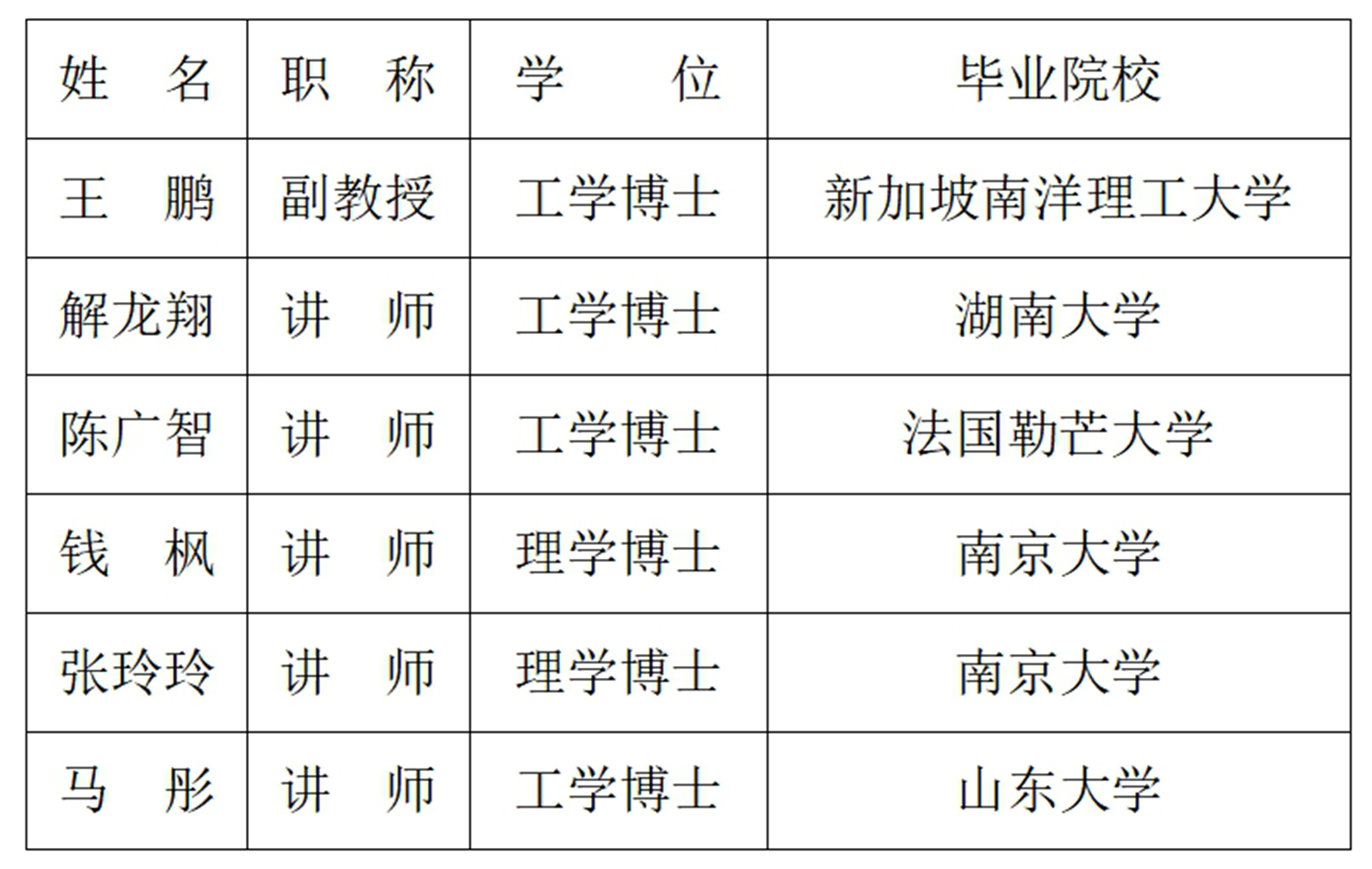
研究内容：

1.功能基元序构声学材料的耦合增强效应与逆向设计：以机器学习与深度学习理论为基础，借助大数据挖掘技术，明晰功能基元间的耦合机制与边界效应，探索声学现象及其物理原理，并归纳总结设计规律。结合数据库系统，实现声学功能材料从“基元-序构-性能”的正向预测与拓扑聚类，建立“声学性能-功能基元+人工序构”的逆向设计理论体系与其优化算法平台。

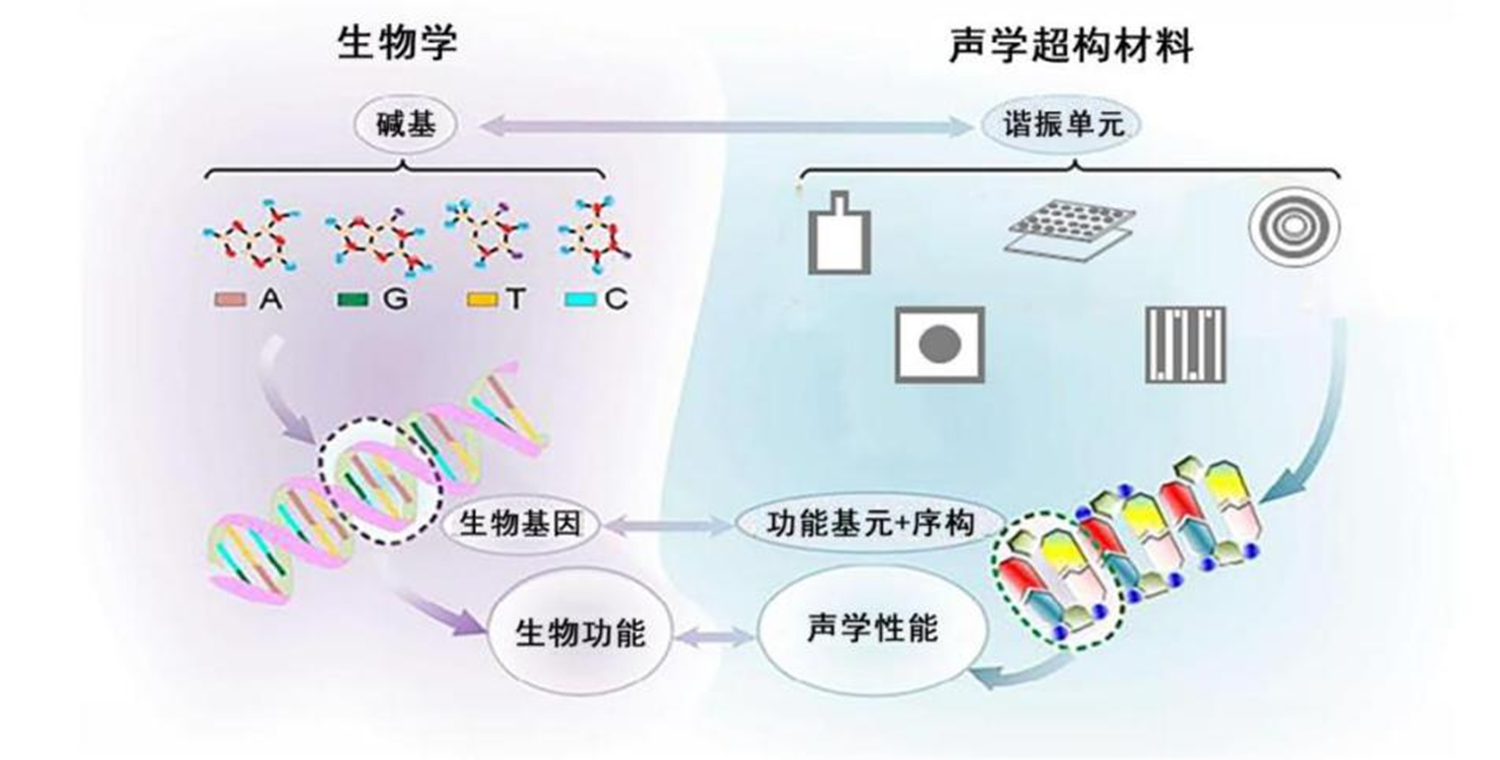
基于类生物基因的符号识别与回归技术

2.基于非线性尾波干涉技术的复杂材料无损检测方法：分析非线性尾波干涉技术损伤检测实验中非线性效应的物理机理；解析非线性声传播方程，建立数值仿真模型进行参数分析；提取可以表征复杂材料微损伤程度的非线性参量，并设计实验进行验证。

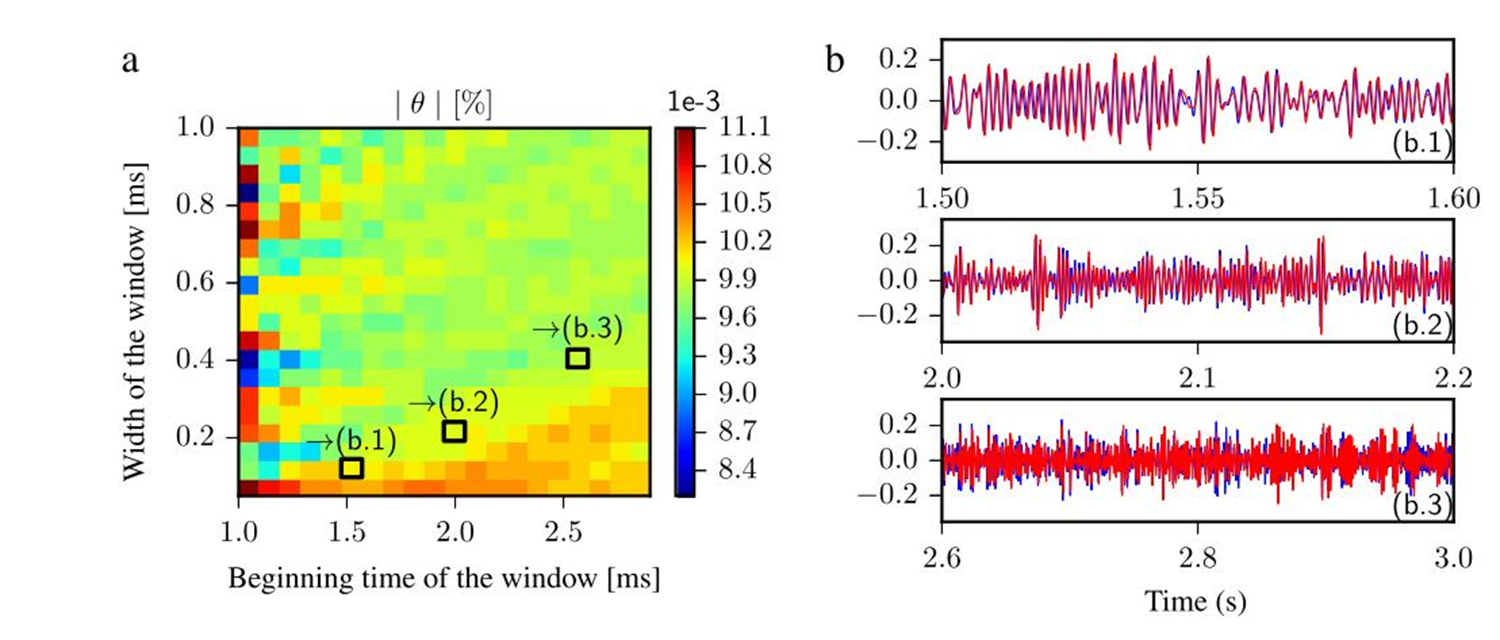
非线性尾波干涉技术仿真实验

3.多空化泡的动力学及非线性特征：构建含有移动的三维多空化泡动力学模型和实验观察空化泡的移动和空化泡之间的吸引和排斥情况，进而研究多空化泡的动力学及其非线性特征。通过实验验证理论模型的准确性和实际可行性，进一步修改理论模型。

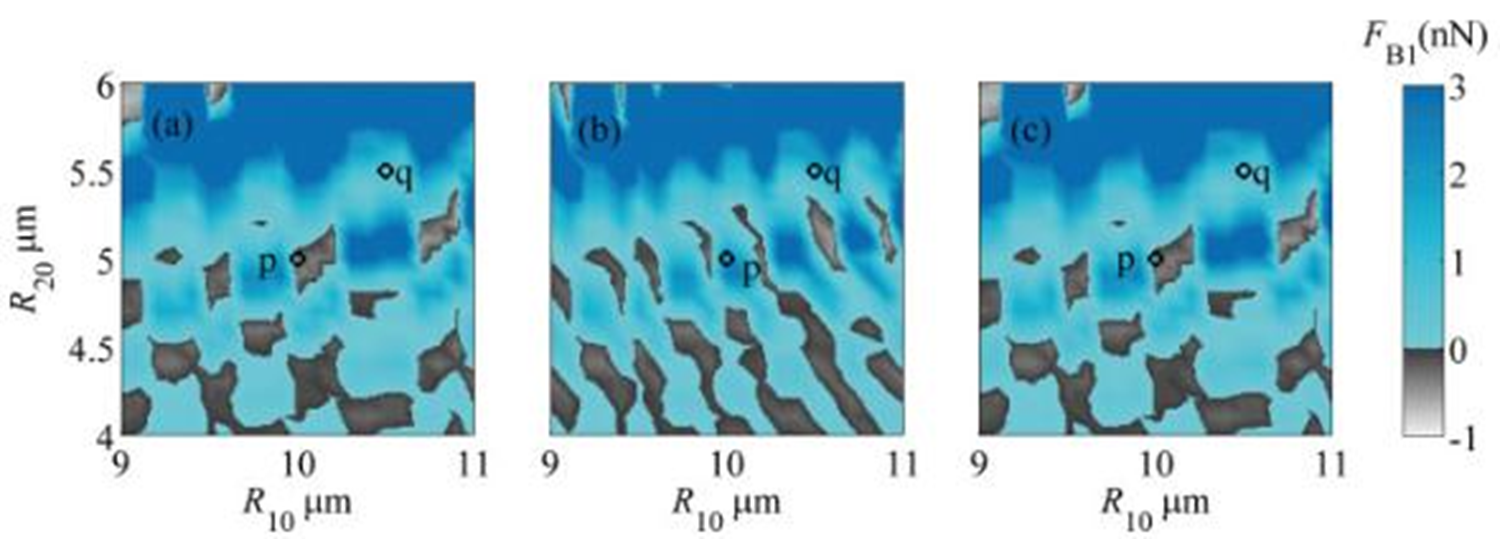
半径相空间中次级Bjerknes力分布的倍周期演化图

4. 分布式可重构声信号分解滤波器组设计：在助听系统中，使用可重构滤波器组进行声信号分解，能够实现匹配不同患者的响度补偿需求。但现有可重构滤波器组的可重构性有限且复杂度高，研究分布式可重构滤波器组设计方法，能有效提升可重构滤波器组的声信号分解的准确度，提升助听系统的响度补偿性能。研究通过优化子带生成模式，克服传统模式对子带独立性控制的约束。通过解决可变滤波器结构、频率扩展结构以及子带分布式独立控制结构的融合设计问题，实现滤波器组的分布式可重构设计。通过对功能结构进行共享设计，对参数进行深入优化，实现全面的复杂度优化设计。

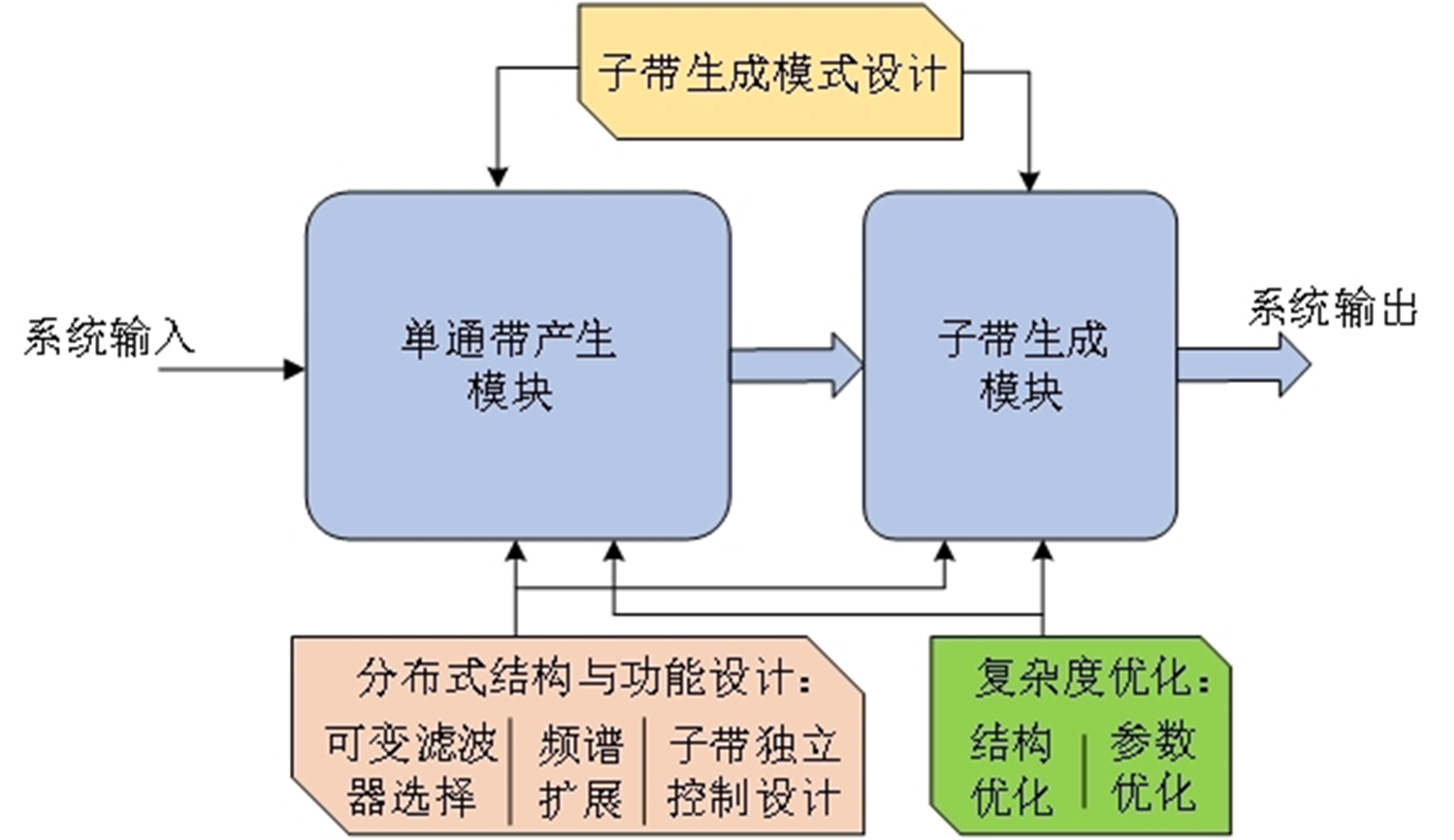
分布式可重构声信号分解滤波器组

代表性论文：

1. Guangzhi Chen; Odile Abraham; Damien Pageot; Olivier Durand; Mathieu Chekroun; Vincent Tournat; Evaluation of nonlinear interface areas in a multiple scattering medium by Nonlinear Coda Wave Interferometry (NCWI): Experimental studies, NDT and E International, 2024, 141: 102992.

2. Le Liu; Longxiang Xie; Weichun Huang; Xiujuan Zhang; Ming-Hui Lu; Yan-Feng Chen; Broadband acoustic absorbing metamaterial via deep learning approach, Applied Physics Letters, 2022, 120(25): 251701-1-251701-6.

3. Y. R. Wu; W. Z. Chen;L. L. Zhang; et al.Pulsation, translation and P1 deformation of two aspherical bubbles in liquid,Journal of The Acoustical Society of America,2022, 151: 888.

4. Y. Shen; W. Z. Chen;L. L. Zhang; Y. R. Wu; et al. The dynamics of cavitation bubbles in a sealed vessel,Ultrasonics Sonochemistry,82: 105865.

5. L. L. Zhang; W. Z. Chen; Y Shen; Y. R. Wu; et al. The nonlinear characteristics of the pulsations, translations and the secondary Bjerknes force,Chaos, Solitons & Fractals,2021, 152: 111322.

6. L. L. Zhang; W. Z. Chen; Y. R. Wu; et al. The repulsive bubble-bubble interaction in an ultrasonic field,Chinese Physics B,2021, 30: 104301.

7. Chen, Guangzhi; Zhang, Yuxiang; Abraham, Odile; Pageot, Damien; Chekroun, Mathieu; Tournat, Vincent; Numerical parametric study of Nonlinear Coda Wave Interferometry sensitivity to microcrack size in a multiple scattering medium, Ultrasonics, 2021, 116(4): 0-106483.

8. Y Shen;L. L. Zhang; Y. R. Wu; W. Z. Chen; et al.The role of the bubble–bubble interaction on radial pulsations of bubbles,Ultrasonics Sonochemistry,2021, 73: 105535.

9. Guangzhi Chen; Damien Pageot; Odile Abraham; Yuxiang Zhang; Mathieu Chekroun; Vincent Tournat; Nonlinear Coda Wave Interferometry: Sensitivity to wave-induced material property changes analyzed via numerical simulations in 2D, Ultrasonics, 2019, 99(-): 105968.

10. Lei, Ji-Rong; Xie, Long-Xiang; Liu, Jian; Band structure analysis of phononic crystals based on the Chebyshev interval method, Journal of The Acoustical Society of America, 2017, 5(142): 3234-3244.

11. Xie Longxiang; Liu, Jian; Huang, Guoliang; Zhu, Wenqing; Xia, Baizhan; A polynomialbased method for topology optimization of phononic crystals with unknown-but-bounded parameters, International Journal for Numerical Methods in Engineering, 2018, 7(114): 777-800.

12. Longxiang Xie; Baizhan Xia; Jian Liu; Guoliang Huang; Jirong Lei; An improved fast plane wave expansion method for topology optimization of phononic crystals, International Journal of Mechanical Sciences, 2017, 120: 181.

13. L. L. Zhang; W. Z. Chen; Y. Y. Zhang; Y. R. Wu; et al.Bubble translation driven by pulsation in a double-bubble system,Chinese Physics B,2020, 29: 034303.

14. Guangzhi Chen; Damien Pageot; Jean-Baptiste Legland; Odile Abraham; Mathieu Chekroun; Vincent Tournat; Numerical modeling of ultrasonic coda wave interferometry in a multiple scattering medium with a localized nonlinear defect, Wave Motion, 2017, 72(-): 228-243.

15. Xie, longxiang; Xia, Baizhan; Huang, Guoliang; Lei, Jirong; Liu, Jian; Topology optimization of phononic crystals with uncertainties, Structural and Multidisciplinary Optimazation, 2017, 6(56): 1319-1339.