刘永，博士，讲师。2020年毕业于上海大学数学系。主要研究方向为随机数值线性代数，目前担任Journal of Computational and Applied Mathematics审稿人。

刘永博士长期从事线性方程组的随机Kaczmarz类迭代算法研究。迄今为止，以第一作者或通讯作者在Applied Numerical Mathematics、Linear Algebra and its Applications、Calcolo和Applied Mathematics and Computation等期刊上发表学术论文7篇，详见https://orcid.org/0000-0002-5569-5765。

近期主要围绕随机Kaczmarz算法和随机Gauss-Seidel算法的块迭代格式展开研究，主要工作如下：

一、关于相容线性方程组的块Motzkin算法研究

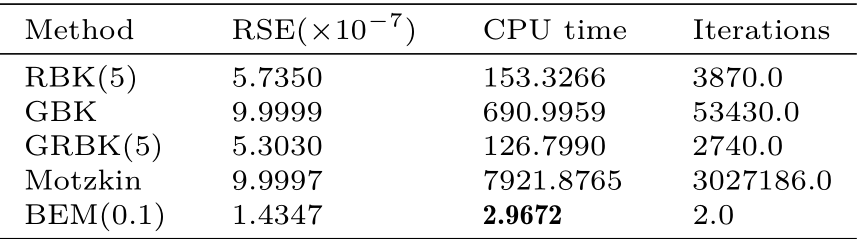
研究大规模相容线性方程组，通过引入相关参数并利用残差向量来控制迭代目标块的大小，构造了块Motzkin算法。该算法在迭代步数和计算时间方面均比现有的随机块Kaczmarz算法、贪心块Kaczmarz算法、Motzkin算法表现优越。例如，针对规模为的paralleltomo图像重构问题，提出的算法只需2.9672秒即可达到预设精度，而其它几种算法则需要较多的计算时间，相关数值结果见表1。这一工作发表在Linear Algebra Appl.，2021，616，178-200。

表1 针对paralleltomo图像重构问题的数值结果

二、关于最小二乘问题的最大残差块Gauss-Seidel算法研究

在图像处理领域，由于噪声的存在，通常需要数值求解一个最小二乘问题来重构图像。随着问题规模的不断扩大，一些现有的Gauss-Seidel型随机迭代算法的收敛速度则会变得比较慢，而块状类型的Gauss-Seidel迭代算法则能有效加速原算法的收敛。刘永博士及其合作者提出了最大残差块及两步Gauss-Seidel算法，并详细分析了这两种算法的收敛性质。研究表明，最大残差块Gauss-Seidel算法比一些现有的块迭代算法，如GRGS、GGS、RGRGS、RaBK在迭代步数和计算时间方面表现更为优秀，并且迭代过程中的目标块的规模更小。例如，针对规模为的seismictomo图像重构问题，最大残差块Gauss-Seidel算法迭代过程中的目标块的规模远小于GBGS算法，但重构效果却优于GBGS算法，相关模拟结果如图1和图2所示。这一工作发表在Calcolo，2021，58，1-32。

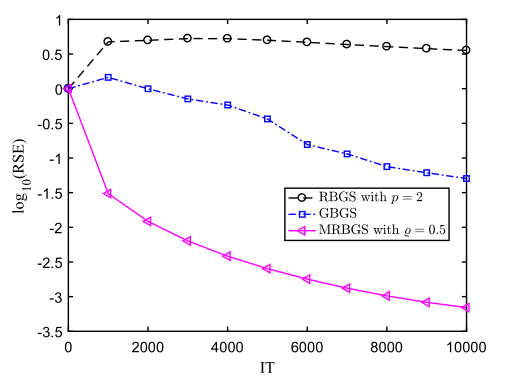
图1 RBGS、GBGS、MRBGS相对解误差随迭代步数的变化曲线

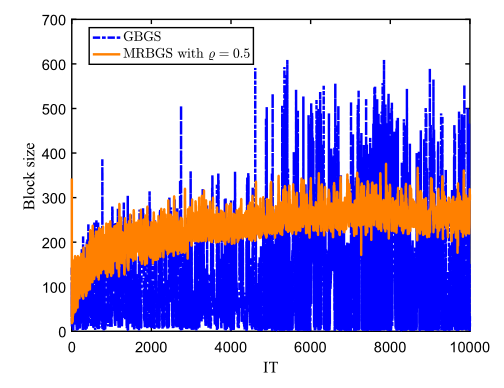
图2 GBGS和MRBGS迭代目标块的大小比较