刘建根，博士，讲师。毕业于中国矿业大学数学学院。博士期间，主持完成江苏省研究生科研与实践创新计划项目以及中国矿业大学博士创新专项基金项目多项，获得江苏省研究生“问题驱动下的数学及应用”学术创新论坛优秀奖，博士研究生国家奖学金和中国矿业大学优秀研究生。目前，担任Applied Numerical Mathematics、Numerical Methods for Partial Differential Equations、Nonlinear Dynamics和Fractals等多家SCI学术期刊特邀审稿人。

刘建根博士长期从事分数阶理论、方法和应用，及孤立子与可积系统方面的研究。以第一作者身份在Journal of Geometry and Physics、Zeitschrift fur Angewandte Mathematik und Mechanik、Fractals、International Journal of Mathematics等国际知名期刊公开发表学术论文30余篇，其中4篇发表在中国数学学会T2类期刊上，13篇发表在中国数学学会T3类期刊，6篇入选ESI“高被引论文”，1篇入选ESI数据库“热点论文”，具体见ResearchGate网站（https://www.researchgate.net/profile/Jian-Gen-Liu）。

近期主要围绕分数阶孤子模型的公式化和可积性指标方面的研究：

一、分数阶孤子模型的公式化问题

利用欧拉-拉格朗日变分技术和半逆方法等多种方法相结合，能够系统地导出Riemann-Liouville分数阶导数意义下的非线性孤子方程。以耦合Burgers型方程组为例并应用以上思想方法，得到时间分数阶耦合Burgers型方程组，为后续研究此模型奠定坚实的理论基础。此项工作发表在：Journal of Geometry and Physics, 169(2021), 104334。

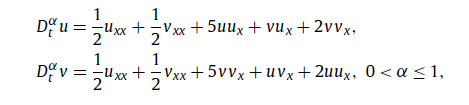
二、分数阶非线性模型的对称、最优系统和守恒律等

通过延伸分数阶Lie对称群法和Noether's定理等相关多种方法，可以比较系统的导出时间或者时间空间分数阶非线性模型的对称、最优系统和守恒律等。同时，借助Erdélyi-Kober分数微分/积分算子，可以将分数阶非线性模型进行降维约化，为后续找到它们的解提供可能。此项工作发表在Journal of Geometry and Physics, 160 (2021) 104000；Fractals, 2021, 29(6), 2150169；International Journal of Geometric Methods in Modern Physics, 18(14) (2021) 2150235。